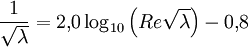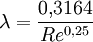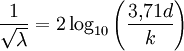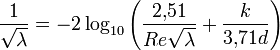Bernoulli entdeckte die Beziehung zwischen der Fließgeschwindigkeit eines Fluides und dessen Druck. Er fand heraus, dass in einem strömenden Fluid (Gas oder Flüssigkeit) ein Geschwindigkeitsanstieg von einem Druckabfall begleitet ist.
Bei der stationären (zeitlich sich nicht verändernden)
Bewegung einer idealen (reibungsfreien) Flüssigkeit, die nur der
Schwerkraft unterworfen ist, gilt für alle Punkte einer Stromlinie,
dass die Summe aus Geschwindigkeitshöhe 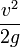 und Druckhöhe
und Druckhöhe
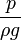 und geodätischer Höhe z konstant ist.
und geodätischer Höhe z konstant ist.
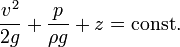
wobei
Multipliziert man die Bernoullische Energiegleichung mit ρ und g, erhält man die Bernoullische Druckgleichung:
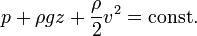
Aus der Bernoullischen Energiegleichung ist ersichtlich, dass zum Beispiel bei einer inkompressiblen Flüssigkeit (ρ = const) eine Geschwindigkeitserhöhung in einer Rohrleitung durch Einengung des Querschnittes zu einer Verminderung des Druckes führen muss, wenn die geodätische Höhe gleich bleibt.
Die erweiterte Bernoullische Energiegleichung setzt sich mit zähen Flüssigkeiten auseinander. Dabei werden die Reibungsverluste berücksichtigt. Die so genannte Verlusthöhe Hv wird empirisch meist durch einen Widerstandsbeiwert ζ (Zeta) mit folgender Funktion berechnet:
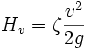
mit
Diese Annahme fußt auf der empirischen Beobachtung, dass die Druckverluste in Rohrleitungen bei turbulenter Strömung mit dem Quadrat der Fließgeschwindigkeit steigen. Die Verlustbeiwerte oder die Summe der Verlustbeiwerte in einem Gesamtsystem setzen sich zusammen aus:
Die erweiterte Energiegleichung lautet daher:
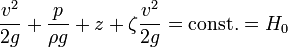
Mit dieser Gleichung können bei Kenntnis der Verlustbeiwerte die üblichen Fragen der Bemessung von Rohrleitungssystemen mit turbulenter Strömung gelöst werden.
Für die Berechnung der Energieverluste wäre zwischen
Einzelverlusten und Verlusten in geraden Rohren zu unterscheiden.
Der Widerstand von Rohrströmungen könnte dabei auch als Widerstandsbeiwert ζ (Zeta) geschrieben werden, lässt sich jedoch noch weiter auflösen (D=Innendurchmesser, L=Länge):
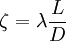
Für die laminare, voll ausgebildete Strömung in einem kreisrunden Rohr kann die Rohrreibungszahl mit der Reynolds-Zahl Re folgendermaßen exakt bestimmt werden:
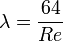
Bei turbulenter Strömung gibt es nur Näherungsformeln zur Bestimmung der Rohrreibungszahl. Dabei sind folgende Fälle zu unterscheiden: