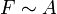 und
und 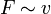 und
und 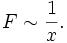
Man stelle sich zwei im Abstand x angeordnete Platten der Fläche A vor. Zwischen diesen Platten befindet sich eine Flüssigkeit, die an beiden Platten haftet. In unserer Vorstellung soll der Raum mit der Flüssigkeit in Schichten unterteilt sein. Wird nun Platte 2 mit der Geschwindigkeit v bewegt, so bewegt sich die Schicht in unmittelbarer Nachbarschaft zu Platte 2 auf Grund der Haftung ebenfalls mit der Geschwindigkeit v. Da Platte 1 ruht, ruht auch ihre Nachbarschicht. Die innenliegenden Flüssigkeitsschichten gleiten mit unterschiedlichen Geschwindigkeiten aneinander vorbei. Die Geschwindigkeit nimmt von der ruhenden Platte zur bewegten zu. Im einfachsten Fall besteht eine lineare Abhängigkeit (siehe Abbildung). Von der obersten, an der Platte haftenden Schicht geht eine Tangentialkraft auf die darunterliegende Schicht aus. Diese bewegt sich folglich mit der Geschwindigkeit v1. Diese Schicht wirkt wiederum auf die darunterliegende Schicht und bewegt sie mit der Geschwindigkeit v2.
Im Experiment lässt sich zeigen, dass die Kraft F, die nötig ist, um Platte 2 zu bewegen, proportional zu ihrer Fläche A, ihrer Geschwindigkeit v und antiproportional zu dem Abstand der Platten x ist:
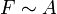 und
und 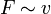 und
und 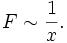
Hieraus ergibt sich
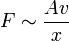
und als Gleichung
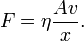
Die Proportionalitätskonstante η ist die dynamische Viskosität. Häufig wird sie auch nur als Viskosität bezeichnet. Ein Stoff hat also die Viskosität 1 Ns/m², wenn bei einer Größe der Platten von 1 m² und einem Plattenabstand von 1 m eine Kraft von 1 N benötigt wird, um die Platten mit einer Geschwindigkeit von 1 m/s gegeneinander zu verschieben.
Für die physikalische Einheit gilt: ![1{\rm N}=[\eta] \cdot\left(\frac{{\rm m}^2\,{\rm m}}{{\rm m}\,{\rm s}}\right) \Rightarrow [\eta] = \frac{{\rm N}\,{\rm s}}{{\rm m}^2}.](a52e7d4f20fe0b2dcff8ac2999946d4d.png)
Ist η unabhängig von der Geschwindigkeit v, so wird die Flüssigkeit als Newtonsche Flüssigkeit bezeichnet. Für diese Flüssigkeiten stellt sich das in Abbildung 2 gezeigte, lineare Geschwindigkeitsprofil ein. Ist η von v abhängig, so bezeichnet man die Flüssigkeit als nicht-newtonsch.
Im Folgenden wird der vereinfachte Zusammenhang gemäß dem
newtonschen Viskositätsgesetz dargestellt, es wird dabei
stets laminare Strömung sowie Temperatur- und
Druckunabhängigkeit der Flüssigkeitseigenschaften angenommen.
Außerdem unterstellte Newton eine lineare Abhängigkeit des
oben erläuterten Geschwindigkeitsgradienten, der auch
Schergeschwindigkeit 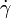 (manchmal auch mit D oder G
bezeichnet) genannt wird:
(manchmal auch mit D oder G
bezeichnet) genannt wird:
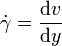
 |
Schubspannungs-Schergeschwindigkeits-Diagramm: 1: dilatantes Fluid 2: Newtonsche Fluid 3: Scherverdünnendes (pseudoplastisches) Fluid 4: Bingham-plastisches Fluid 5: Casson-plastisches Fluid |
Verknüpft man dies mit der Schubspannung τ, erhält man folgenden Zusammenhang für die dynamische Viskosität:
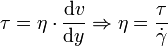
Die Schubspannung τ ergibt sich aus der die Strömung bewirkenden Kraft bezogen auf die betroffene Angriffsfläche, die sich mit maximaler Geschwindigkeit bewegt. η wird bei newtonschen Flüssigkeiten als Konstante angesehen. Darüber hinaus wird das Verhältnis zwischen der dynamischen Viskosität η und der Dichte ρ definiert als kinematische Viskosität.
kinematische Viskosität: 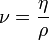 dynamische
Viskosität:
dynamische
Viskosität: 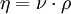
Viele Substanzen folgen diesem Gesetz jedoch nicht, sondern zeigen ein zeit- oder schergeschwindigkeitsabhängiges Verhalten. Dabei unterscheidet man verschiedene Arten der Abweichung:
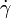
Derartige Fluide bezeichnet man als nichtnewtonsche Fluide.
Im allgemeinen Fall muss das Schergefälle 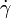 aus dem Scherwinkel in der Flüssigkeit berechnet
werden und nicht über den Geschwindigkeitsgradienten.
aus dem Scherwinkel in der Flüssigkeit berechnet
werden und nicht über den Geschwindigkeitsgradienten.
Die SI-Einheit der
![[\eta] = \frac{\rm Ns}{\rm m^2}](4909a229ccf416386a5f8c2904018654.png)
![[\nu] = \frac{\rm m^2}{\rm s}](02bf4fd293d056d8c0ebc96c381aa866.png)
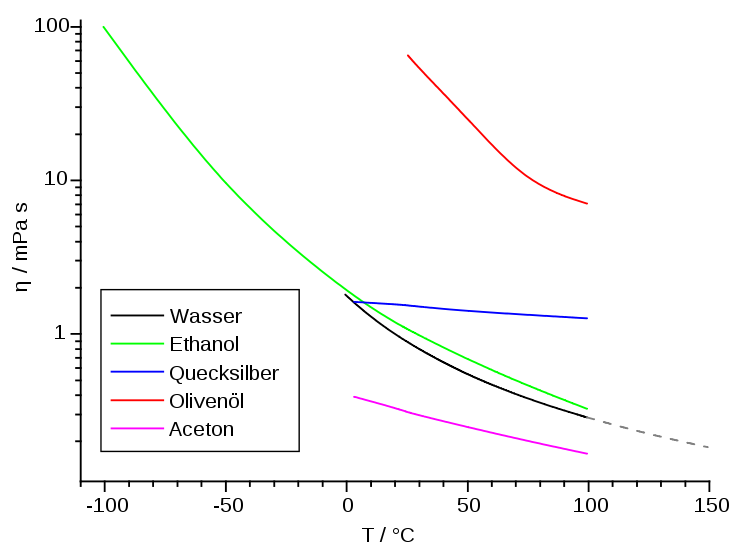
In der Praxis wird für die dynamische Viskosität neben der Pa·s (Pascalsekunde) außerdem der tausendste Teil der SI-Einheit mPa·s (Millipascalsekunde) für Medien niedriger Viskosität verwendet.
Im CGS-System wird die dynamische Viskosität in Poise (P) gemessen, wobei 1 Ns/m2 = 1 Pa·s = 10 Poise und 1000 Centipoise = 1000 cP = 1 kg/ms, und die kinematische Viskosität in Stokes (St), 1 St = 10−4 m2/s.
Die Reynolds-Zahl (Formelzeichen: Re) ist eine nach dem Physiker Osborne Reynolds benannte dimensionslose Kennzahl. Sie wird in der Strömungslehre verwendet und stellt das Verhältnis von Trägheits- zu Zähigkeitskräften dar (bzw. das Verhältnis von spezifischer Impulskonvektion zu Impulsdiffusion im System). Daraus ergibt sich, dass das Turbulenzverhalten geometrisch ähnlicher Körper bei gleicher Reynoldszahl identisch ist. Diese Eigenschaft erlaubt z.B. realitätsnahe Modellversuche im Windkanal oder Wasserkanal.
 mit
mit 
Die einzelnen Formelzeichen stehen für folgende Größen:
 –
charakteristische Dichte des Fluides (kg m−3)
–
charakteristische Dichte des Fluides (kg m−3) –
charakteristische Strömungsgeschwindigkeit des Fluides
gegenüber dem Körper (m s−1)
–
charakteristische Strömungsgeschwindigkeit des Fluides
gegenüber dem Körper (m s−1) –
charakteristische Länge des Gegenstandes (m)
–
charakteristische Länge des Gegenstandes (m)Die charakteristische Länge, auch Bezugslänge genannt, kann prinzipiell frei gewählt werden. Beim Vergleich zweier Strömungen muss diese Länge jedoch gleicher Art sein. Bei Strömungskörpern wird als Bezugslänge üblicherweise die Länge des Körpers in Strömungsrichtung gewählt. Bei Widerstandskörpern ist die Breite oder Höhe quer zur Strömungsrichtung üblich. Bei Rohrströmungen Radius oder Durchmesser des Rohres, bei Gerinnen die Tiefe oder die Breite an der Gerinne-Oberfläche.
 –
charakteristische dynamische
Viskosität des Fluides (kg s−1 m−1)
–
charakteristische dynamische
Viskosität des Fluides (kg s−1 m−1) –
charakteristische kinematische
Viskosität des Fluides (m2 s−1)
–
charakteristische kinematische
Viskosität des Fluides (m2 s−1)eine mathematische Gleichung, die bei Strömungsvorgängen
die Erhaltung einer physikalischen Größe (z. B.
Flüssigkeitsmenge, elektrische Ladung) zum Ausdruck bringt. Die
Dichte dieser Größe in einem Raumgebiet kann sich nur
dadurch ändern, dass etwas aus dem Gebiet heraus- oder in es
hineinfließt.
Kontinuitätsgleichung:![]()
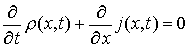
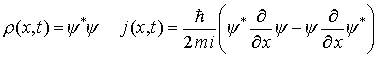
Die Kontinuitätsgleichung drückt die Erhaltung der Materie
aus. Die zeitliche Änderung der Wahrscheinlichkeitsdichte ![]()
![]() wird
durch die Wahrscheinlichkeitsstromdichte j erzeugt
wird
durch die Wahrscheinlichkeitsstromdichte j erzeugt
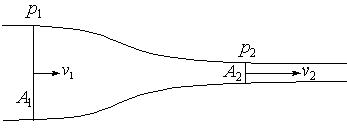
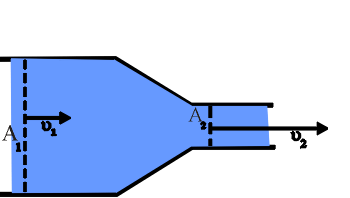
Abbildung1: Skizze zur Kontinuitätsgleichung. Da
die Flüssigkeit nicht
komprimiert werden kann, muß das pro Zeiteinheit in beiden Teilen
des Rohres fließende
Volumen gleich sein.
Das pro Zeiteinheit fließende Volumen ![]() ist
ist
![]()
Da keine Teilchen verloren gehen können und wir von Kompression
absehen, müssen beide
Volumina gleich sein und es ergibt sich die sog. Kontinuitätsgleichung:
![]()
Die Gleichung hat wichtige Konsequenzen.

Abbildung2: Skizze zur Kontinuität im Blutkreislauf
Wird die Kontinuitätsgleichung auf den menschlichen Blutkreislauf angewandt, so wird die geringe Fließgeschwindigkeit in den Kapillaren verständlich, ohne die lebensnotwendige Difusionsvorgänge nicht in ausreichendem Maße stattfinden könnten.
Der Durchmesser der Aorta beträgt ungefähr 2,3cm . Ihre Querschnittsfläche beträgt dann 4 cm2.
Geht man davon aus , daß in einer Minute ungefähr 5 Liter Blut durch die Aorta strömen, so ergibt sich aus obiger Gleichung (3.10) eine mittlere Strömungsgeschwindigkeit von 20,8 cm · s-1. Geht man von einer Gesamtquerschnittsfläche der Kapillaren von 4800 cm2 aus, so erhält man rechnerisch mit (3.10) eine mittlere Strömungsgeschwindigeit von 0,017 cm ·s-1.
Eingesetzt in
![]()
erhält man: 4 cm2 ·20,8 cm·s-1 = 83,2cm3·s-1
4800cm2 ·0,017 cm·s-1 = 83,2cm3·s-1