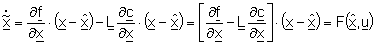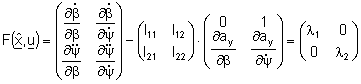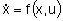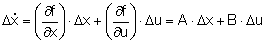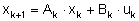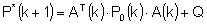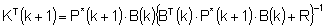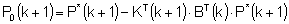PKW-Fahrdynamikreglerentwicklung mittels Zustandsraummodell am Beispiel eines 4WS-Prototypen
Dipl. Ing. Alfred Pruckner
Dipl. Ing. Francis Noutsa Noufele
Sven Fischer
Mustapha Khajjou
Institut für Kraftfahrwesen Aachen
RWTH Aachen
Einführung
Fahrzustandserkennung
Fahrzustandsregelung
Zusammenfassung und Ausblick
Literatur
Einführung
Der vorliegende Beitrag beschäftigt sich mit der Möglichkeit der
Fahrzustandsbeobachtung und darauf aufbauend der Fahrzustandsregelung
mittels nichtlinearem Zweispurmodell mit Zustandsrückführung.
Die Entwicklung der Beobachter- und Reglerstruktur basiert auf dem
sogenannten 'Virtuellen Prototyping', welches die Verbindung von
Mehrkörperdynamiksimulationsprogramm (MKS) und Regelungstechnik Software
Tool (RTS) darstellt. Das MKS Modell ersetzt darin die realen
Fahrversuche auf der Teststrecke und liefert so den Input für die
Software, welche als automatisch generierter C-Code aus dem RST erzeugt
wird.
In einer Weiterentwicklung des 'Virtuellen Prototyping' wird am Institut
für Kraftfahrwesen das 'Software Rapid Prototyping' entwickelt, welches
die Benützung des automatisch generierten C-Codes auf beliebigen
Steuerelektroniken ermöglicht, um so eine schnelle und effiziente
Verbindung zu realen Fahrversuchen auf der Teststrecke zu gewährleisten.
Der in diesem Beitrag entwickelte Fahrzustandsbeobachter zur Erfassung
des Fahrzeugschwimmwinkels wurde mittels 'Virtuellem Prototyping'
entwickelt, die Güte der Schwimmwinkelerkennung wird mit den Ergebnissen
eines Einspurmodells verglichen.
Die Darstellung des Fahrzeugverhaltens durch ein Zustandsraummodell
ermöglicht schließlich mit den Hilfsmitteln der Regelungstechnik eine
optimierte Regelung des Fahrzeugverhaltens, was wiederum im Vergleich
mit bisher üblichen Einspurfahrzeugmodell-Regelungen gezeigt wird.
Fahrzustandserkennung
Heute übliche Fahrzustandserkennung basiert auf dem sogenannten
Einspurmodell. In diesem Fahrzeugmodell wird eine lineare
Reifencharakteristik angenommen, außerdem wird die Schwerpunkthöhe zu
null gesetzt, weshalb die Räder einer Achse auf ein Rad reduziert werden
können.
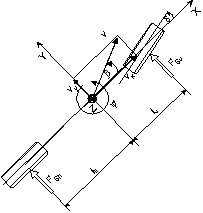
Abb.1: Lineares Einspurmodell
Mit diesen Annahmen sowie der weiteren Vereinfachung von kleinen Winkeln
lassen sich die Fahrzustandsgrößen Schwimmwinkel b und
Gierwinkelgeschwindigkeit
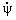
als Differentialgleichungen abhängig von verschiedenen
Fahrzeugparametern sowie der Fahrzeuggeschwindigkeit und dem vorderen
bzw., wenn vorhanden, dem hinteren Lenkwinkel darstellen.
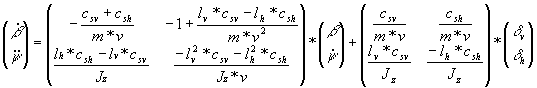
Gl. 1
Diese Differentialgleichungen lassen sich auch in Form einer in der
Regelungstechnik üblichen Zustandsraumgleichung darstellen (Gl. 2),
wobei x den Zustandsvektor (Schwimmwinkel und
Gierwinkelgeschwindigkeit), u den Eingangsvektor (vorderer und hinterer
Lenkwinkel), A die Systemmatrix und B die Eingangsmatrix bezeichnt.
Mit einer für die Erstellung von automatischem C-Code notwendigen
Diskretisierung (Gl. 4 & Gl. 5) kann diese Zustandsraumdarstellung
im RTS Programm MATRIXx abgebildet werden.
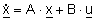
Gl. 2
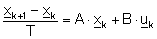
Gl. 3
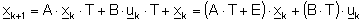
Gl. 4
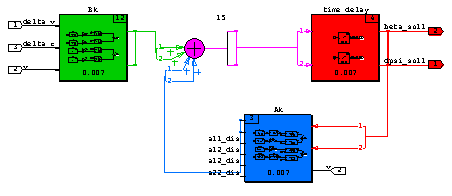
Abb.2: MATRIXx Modell des diskreten, linearen Einspurmodells
Mit Hilfe des 'Virtuellen Prototypings' wird aus dem erstellten
Einspurmodell automatisch C-Code generiert, welcher in einer
ADAMS-Simulation mit den Messdaten aus dem Fahrzeugmodell beschickt wird
und die Beobachteten Größen bzw. die Stellgröße für eine eventuelle
Regelung an das Modell zurück liefert.
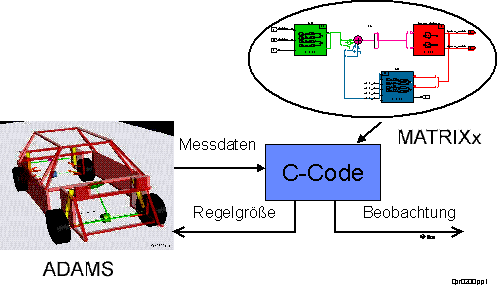
Abb.3: Virtuelles Prototyping
Mit dieser Methode ist ein Vergleich der tatsächlich auftretenden
Zustandsgrößen aus dem MKS Programm ADAMS mit den geschätzten
Einspurmodelldaten sehr schnell und flexibel gestaltbar.
Die folgende Abb. zeigt den Vergleich der beobachteten Zustandsgrößen
und der 'realen' Simulationswerte aus ADAMS. Auf trockener Fahrbahn
genügt das Einspurmodell den nötigen Anforderungen, auf glatter Fahrbahn
jedoch versagt das lineare Einspurmodell aufgrund der
Modellvereinfachungen (Abb.
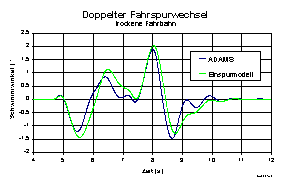
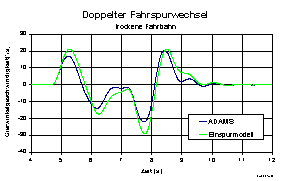
Abb.4: Zustandsgrößenbeobachtung, doppelter Fahrspurwechsel, trockene Fahrbahn
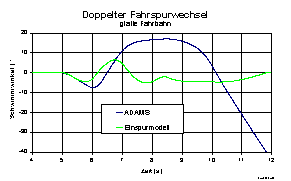
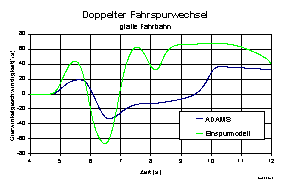
Abb.5: Zustandsgrößenbeobachtung, doppelter Fahrspurwechsel, glatte Fahrbahn
Zur Verbesserung der Zustandsbeobachtung wird ein Zweispurmodell mit
integriertem HSRI-Reifenmodell verwendet, welches die aktuelle
Schräglaufsteifigkeit aus den vorliegenden Messgrößen anpasst. Darüber
hinaus wird der aktuelle Straßenreibwert aus den Reifenkräften des
HSRI-Modells im Vergleich mit den tatsächlichen Kräften geschätzt und
schließlich eine Rückführung der Zustandsgrößen ähnlich dem linearen
Luenbergerbeobachters integriert (Abb.).
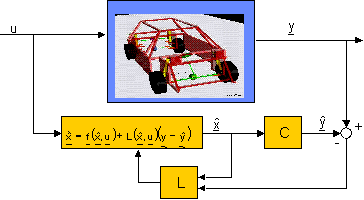
Abb.6: Nichtlineare Fahrzustandsbeobachtung
Die geschätzten Zustandsgrößen des nichtlinearen Fahrzeugmodells
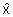
können sowohl von den Zustandsgrößen als auch von den Eingangsgrößen u
nichtlinear abhängen. Aus den geschätzten Zustandsgrößen können mit
Hilfe der Messgleichung C die geschätzten Messgrößen
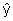
berechnet werden und mit den realen Messwerten y über die Matrix L
abgeglichen werden. Abb. zeigt den prinzipiellen Zusammenhang der
nichtlinearen Zustandsraumbeobachtung.
Da die Zustandsgrößen nicht exakt vorliegen, wird die
Zustandsraumgleichung und die Messgleichung um die geschätzten Größen
linearisiert:
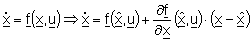
Gl. 5
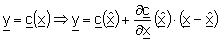
Gl. 6
Von dieser linearisierten Zustandsraumdarstellung wird die geschätzte
Zustandsraumgleichung sowie der Abgleich aus den Messgrößen abgezogen,
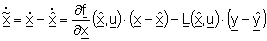
Gl. 7
so dass nach Einsetzen der Messgleichung eine Differentialgleichung für den Schätzfehler
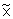
entsteht. Die Matrix
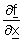
bezeichnet die sogenannte Jakobi-Matrix des Systems:
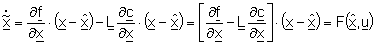
Gl. 8
Diese Differentialgleichung F des Schätzfehlers soll möglichst rasch mit
abklingendem Verhalten gegen Null gehen, was mit der Wahl negativer
Eigenwerten l im kontinuierlichen Fall bzw. mit Eigenwerten innerhalb
des Einheitskreises im diskreten Fall gegeben ist.
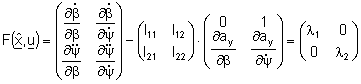
Gl. 9
D.h. durch die Wahl der Eigenwerte der vorliegenden
Differentialgleichung können mittels Koeffizientenvergleich die
Matrizenelemente l der Korrekturmatrix L in jedem Berechnungsschritt
berechnet werden, um so den Schätzfehler möglichst klein werden zu
lassen und die Zustandsgrößen möglichst exakt zu bestimmen. Die folgende
Abb. zeigt einen Vergleich der Güte des Beobachtermodells mit dem zuvor
gezeigten Einspurmodell.
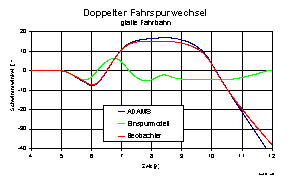
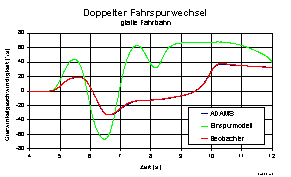
Abb. 7: Zustandsgrößenbeobachtung, doppelter Fahrspurwechsel, glatte Fahrbahn
Um den vorhandenen Zustandsraumbeobachter auch im realen Fahrbetrieb
flexibel und effizient einsetzen zu können, wird mittels 'Software Rapid
Prototyping' der erzeugte C-Code direkt in einen handelsüblichen
Steuerrechner auf Basis eines C-167 µ-Controllers implementiert. Die
Messdaten für den Zustandsraumbeobachter wird nun direkt aus dem
Testfahrzeug mittels geeigneter Sensorik erfasst, die beobachteten
Größen werden mit Hilfe eines Messrechners aufgezeichnet.
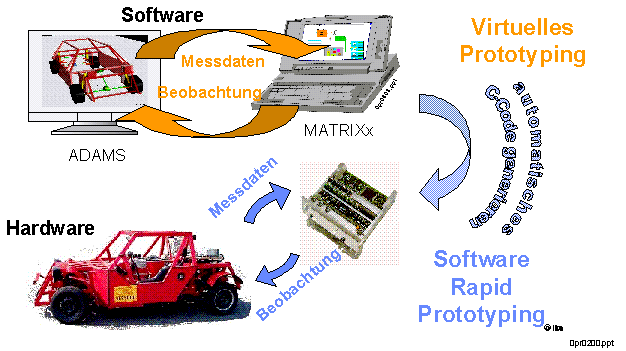
Abb.8: Software Rapid Prototyping
Abb. zeigt das Ergebnis eines Sinuslenkmanövers auf trockener Fahrbahn
im Vergleich zum Einspurmodell und einem Zweispurmodell ohne
Zustandsgrößenrückführung. Deutlich ist die Verbesserung der Beobachtung
durch das Zustandsraummodell zu erkennen, für weitere
Verbesserungsdarstellungen sind Fahrversuche auf glatter Fahrbahn noch
durchzuführen.

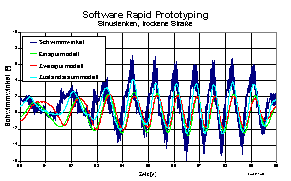
Abb. 9: Software Rapid Prototyping, Schwimmwinkelbeobachtung
Fahrzustandsregelung
Aus dem vorliegenden Zustandsraummodell ist mit den Mitteln der
Regelungstechnik eine geeignete Zustandsgrößenregelung machbar. Dazu
wird ein optimaler Zustandsregler ausgewählt, da er gute
Dämpfungseigenschaften besitzt und mit Hilfe des Algorithmus des
Kalman-Filters auch auf zeitvariante Prozesse übertragen werden kann.
Zunächst wird die vorliegende nichtlineare Zustansraumgleichung um den aktuellen Arbeitspunkt linearisiert bzw. diskretisiert
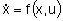
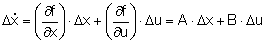
Gl. 11
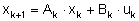
Gl. 12
Der Regler wird dabei so gewählt, dass er optimal im Sinne eines
definierten Gütefunktionals ist. Daraus erhält man einen linearen,
zeitvarianten Regler mit folgender Struktur:
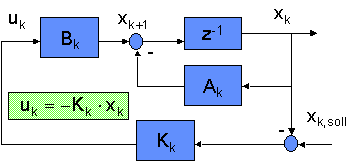
Abb.10: Fahrzustandsregelung
D.h., es muss eine geeignete Rückführmatrix K gefunden werden, welche
aus der Differenz der Soll- und Ist- Zustandsgröße die optimale
Stellgröße, im vorliegenden Fall der hintere Lenkwinkel, berechnet.
Das Gütekriterium führt auf die Riccati-Gleichung, aus deren Lösung sich
die Rückführmatrix bestimmen lässt. Dafür wurde der Algorithmus zur
Berechnung des Kalman-Filters gewählt, was aufgrund der Symmetrie des
Reglers- und Beobachterproblems zulässig ist.
Der Algorithmus lautet:
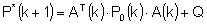
Gl. 13
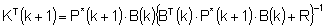
Gl. 14
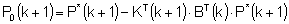
Gl. 15
mit Q und R als wählbare Gewichtungsmatrizen.
Aus dem Algorithmus folgt für jeden Berechnungsschritt die
Rückführmatrix K, welche die Stellgröße (hinterer Lenkwinkel) bestimmt.
Die Ergebnisse dieser Zustandsregelung zeigt das folgende simulierte
Fahrmanöver eines doppelten Fahrspurwechsels auf glatter Fahrbahn. Das
ungeregelte Fahrzeug schleudert durch das Manöver was an dem großen
vorderen Lenkwinkel und der Fahrspur (Abb. 11) sowie dem Schwimmwinkel
(Abb. 12) zu erkennen ist.

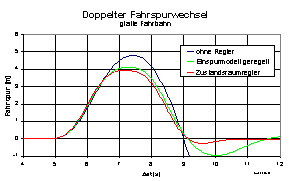
Abb.11: Fahrzustandsregelung, Lenkwinkel vorne und Fahrspur, doppelter Fahrspurwechsel, glatt
Das Fahrzeug mit der Zustandsraumregelung schafft den Fahrspurwechsel
erwartungsgemäß besser, was an der besseren Erkennung des aktuellen
Fahrzustandes und der optimalen Regelung liegt. Wahrend das Fahrzeug mit
einer gewöhnlichen Einspurmodellregelung den Schwimmwinkel des
Einspurmodells möglichst gering hält, wächst der reale Schwimmwinkel
stärker an als im Fall der Zustandsraumregelung, wo der besser
beobachtete Schwimmwinkel gegen Null geregelt wird (Abb. 13).
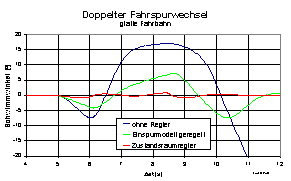
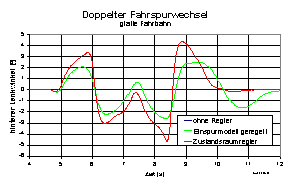
Abb.12: Fahrzustandsregelung, Schwimmwinkel und Lenkwinkel hinten, doppelter Fahrspurwechsel, glatt
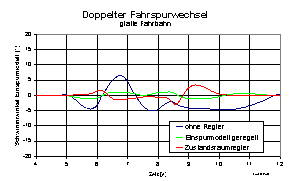
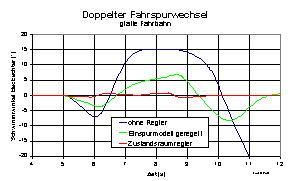
Abb.13: Fahrzustandsregelung, Schwimmwinkel Einspurmodell und beobachtet, doppelter Fahrspurwechsel, glatt
Prinzipiell kann mit dem gezeigten Zustandsraumregler jede Stellgröße,
welche in den Zustandsgleichungen eingebracht werden kann, zur Regelung
herangezogen werden. So könnte auch z.B. ein zusätzlicher vorderer
Lenkwinkel zur Fahrzeugstabilisierung genutzt werden. Durch eine
Formulierung der Reifenlängskräfte in Abhängigkeit des Längsschlupfes
und dessen Einfluss auf die Seitenkräfte könnte auch eine Regelung der
Gierwinkelgeschwindigkeit mittels Bremseingriff in Kombination mit
stabilisierendem Lenkeingriff an Vorder- und/oder Hinterachse vorgesehen
werden.
Zusammenfassung und Ausblick
Die gezeigte Zustandsraumbeobachtung eines Fahrzeuges erlaubt mit den
vorhandenen Messgrößen eines Fahrzeuges den Schwimmwinkel in
Grenzbereichen, wo das lineare Einspurmodell versagt, sehr genau zu
erfassen. Diese Fahrzustandsbeobachtung stellt eine kostengünstige
Alternative zu aufwendiger Sensorik dar und erlaubt den Schritt zu
integrierter Fahrzustandsregelung, welche verschiedene Anforderungen
einer Fahrzeugregelung unter regelungstechnischen Gesichtspunkten
aufstellen lässt.
Die Methode des 'Virtuellen Prototypings' stellt dabei im Zusammenspiel
mit dem 'Software Rapid Prototyping' eine schnelle und flexible
Möglichkeit dar, verschieden komplexe Ansätze zu realisieren,
analysieren und zu optimieren. Das Zusammenspiel der einzelnen Systeme
kann jederzeit sowohl simulationstechnisch als auch darauf aufbauend auf
der Teststrecke nachvollzogen werden. Der Einsatz handelsüblicher
Steuerrechner ermöglicht zudem realitätsnähere Testbedingungen für
Software und Elektronik-Hardware.
Die gezeigte Methode der Hinterradlenkregelung wird derzeit am Institut
für Kraftfahrwesen in einem Prototypenfahrzeug installiert und in naher
Zukunft für verschiedene Anforderungen und verschiedenen
Straßenzuständen getestet.
Literatur
[ADA94] N.N.
ADAMS / Solver - Reference Manual, Version 8.0
Mechanical Dynamics, Inc.
Ann Arbor, Michigan, 2. Auflage 1994
[DIE91] DIEKMANN, T.
Ein neuartiger Ansatz zur Bestimmung der Kraftschlußbedingungen im Reifen/Fahrbahn-Kontakt
3. VDI- Fachtagung Reifen- Fahrwerk- Fahrbahn, Hannover, 1991
[FÖL93] FÖLLINGER, OTTO
Nichtlineare Regelungen II
R.Oldenbourg Verlag
München, Wien, 7. Auflage 1993
[ISE92] ISERMANN, R.
Identifikation dynamischer Systeme
Springer-Verlag, Berlin, Heidelberg, London, Paris, Tokio, 2. Auflage 1992
[KOR94] KORTÜM, W., LUGNER, P.
Systemdynamik und Regelung von Kraftfahrzeugen
Springer-Verlag, Berlin, Heidelberg 1994
[PRU97] PRUCKNER, A.
Analysis of Dynamic Driving Control (DDC) Systems on a full vehicle Model in ADAMS, ADAMS Users Conference, Marburg 1997
[PRU98] PRUCKNER, A.
Virtuelles Prototyping zur Entwicklung von Fahrwerkregelungssystemen mit ADAMS und MATRIXx, 7. Aachener Kolloquium, Aachen 1998
[WAL96] WALLENTOWITZ, H.
Vertikal-/Querdynamik von Kraftfahrzeugen
Umdruck zur Vorlesung 'Kraftfahrzeuge II'
Institut für Kraftfahrwesen, RWTH Aachen, Aachen, 1996

 als Differentialgleichungen abhängig von verschiedenen
Fahrzeugparametern sowie der Fahrzeuggeschwindigkeit und dem vorderen
bzw., wenn vorhanden, dem hinteren Lenkwinkel darstellen.
als Differentialgleichungen abhängig von verschiedenen
Fahrzeugparametern sowie der Fahrzeuggeschwindigkeit und dem vorderen
bzw., wenn vorhanden, dem hinteren Lenkwinkel darstellen.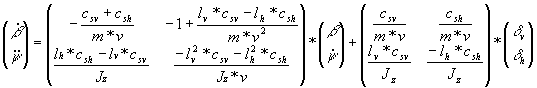
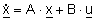
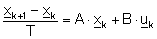
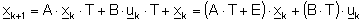







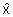 können sowohl von den Zustandsgrößen als auch von den Eingangsgrößen u
nichtlinear abhängen. Aus den geschätzten Zustandsgrößen können mit
Hilfe der Messgleichung C die geschätzten Messgrößen
können sowohl von den Zustandsgrößen als auch von den Eingangsgrößen u
nichtlinear abhängen. Aus den geschätzten Zustandsgrößen können mit
Hilfe der Messgleichung C die geschätzten Messgrößen 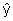 berechnet werden und mit den realen Messwerten y über die Matrix L
abgeglichen werden. Abb. zeigt den prinzipiellen Zusammenhang der
nichtlinearen Zustandsraumbeobachtung.
berechnet werden und mit den realen Messwerten y über die Matrix L
abgeglichen werden. Abb. zeigt den prinzipiellen Zusammenhang der
nichtlinearen Zustandsraumbeobachtung.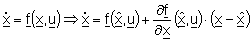
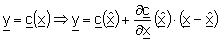
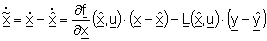
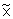 entsteht. Die Matrix
entsteht. Die Matrix 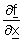 bezeichnet die sogenannte Jakobi-Matrix des Systems:
bezeichnet die sogenannte Jakobi-Matrix des Systems: